The Super Bowl Overtime Cointoss: Should the 49ers Have Deferred?
Photo Credit: Ezra Shaw/Getty Images
Super Bowl LVIII certainly did not disappoint. The big game set the record for average Super Bowl viewership at 123.7m and included a thrilling overtime period.
Before digging into today’s analysis, let’s start with some history on the overtime rules. After the Chiefs’ 42-36 win over the Bills in January 2022, when Patrick Mahomes marched his team downfield and completed an 8-yard touchdown pass to Travis Kelce for the win on the first overtime possession, the NFL made a change to its playoff overtime rules. The coin toss was carrying too much weight: the team who won the toss had a significant advantage, electing to receive and having a chance to end the game without the other team touching the ball. However, the new playoff overtime rules now allow the second offense to have a chance, even if the first offense scores a touchdown.
Now back to Sunday. After winning the coin toss in overtime, the 49ers elected to take the ball. They kicked a field goal and watched Mahomes do his thing - another game winning touchdown drive. What was the right decision for the 49ers - electing to kick or receive?
To answer this, I’ve broken each drive into five possibilities: touchdown, field goal make, field goal miss, punt, and turnover (any of interception, fumble, turnover on downs). Safeties did not make a significant enough dent in the probability distribution to be included. I used 2023 regular season data for the 49ers and Chiefs on both offense and defense to find the probability that their drives end in each of those five outcomes. Regular season drives that ended in the clock running to zero at the end of a half were prorated into the five categories. I then averaged the 49ers on offense with the Chiefs on defense to determine the 49ers’ offensive outcome probabilities against the Chiefs, and averaged the Chiefs on offense with the 49ers on defense to determine the Chiefs’ offensive outcome probabilities against the 49ers.
The probabilities are showcased in Table 1 below.
Table 1: Drive outcome probabilities for Super Bowl LVIII
Due to factors similar to those that made the 49ers a 1.5-point favorite before the game, the probabilities of the 49ers' outcomes in the matchup appear more favorable than those of the Chiefs in Table 1. I will consider the sensitivity in those initial assumptions during the second and third iterations of my analysis.
Table 1 contains the standard drive outcome probabilities, but there are three non-standard cases that could arise in overtime that need to be addressed:
The offense needs to score a touchdown. In this scenario I divided the punt and field goal probabilities evenly between touchdown and turnover.
The offense only needs a field goal to win. Here, I shifted 5% from each of turnover and punt to field goal and shifted all but 5% of touchdown to field goal (the latter doesn’t impact the win probability but makes the tables more accurate).
The offense cannot punt (is down by 3). In this scenario I split punt evenly between touchdown, field goal, and turnover.
The probabilities of the three non-standard cases are stated in Table 2 below.
Table 2: Non-standard drive outcome probabilities for Super Bowl LVIII.
Now that we’ve laid out the outcome probabilities of any given drive, let’s look at the ten ways the game can progress in overtime, outlined in Table 3.
Table 3: The ten ways the game can progress under the new overtime rules.
Table 3 contains the assumption that if the first team scores a touchdown and the second team scores a touchdown, then the second team will go for the two-point conversion to win the game. The assumption is statistically sound as two-point conversions have been successful 50% of the time, so taking that 50/50 chance is a better option than kicking the extra point and letting the opponent win the game with just a field goal. The Chiefs confirmed after the game that this was their plan had the 49ers scored a touchdown on their first overtime possession.
Of the ten scenarios laid out in Table 3, six scenarios end the game and four scenarios allow the game to continue. The six that end the game can be priced using the probabilities in Tables 1 and Table 2. The four that allow the game to continue turn into infinite geometric sequences with the multiplier being the product of the non-score probabilities of each possessing team. I summed up the sequence for the field goal + field goal example and used that sum as a proxy for the other three continuation scenarios (missed field goal, punt, and turnover), which have different expected starting field positions than a kickoff.
Base Case Results
Table 4 displays the outcomes when the 49ers possess the ball first, while Table 5 illustrates the results when the Chiefs have the initial possession (the orange cells mark the 49ers’ win probabilities, whereas the yellow cells mark the Chiefs’ win probabilities).
Table 4: Outcome and win probabilities if the 49ers take the ball first.
Table 5: Outcome and win probabilities if the Chiefs have the ball first.
As we can see in Table 4 and Table 5, according to the base case probabilities, the 49ers’ chance of winning the Super Bowl dropped from 61.4% to 46.8% when they decided to receive the ball in overtime, rather than deferring to the second possession.
Adjusting for the 49ers Injuries
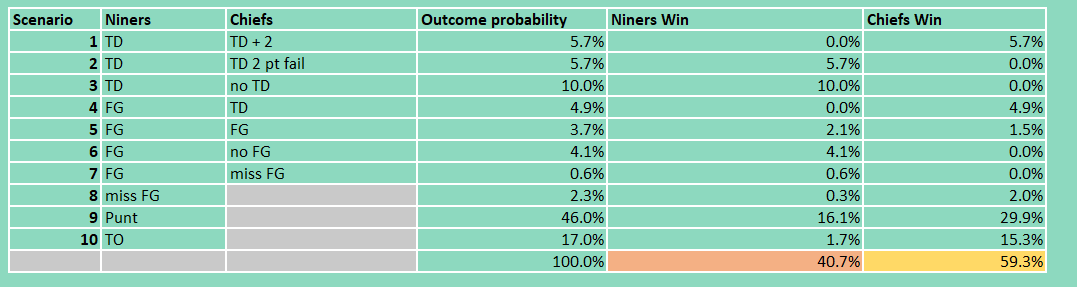
The 49ers had some notable injuries during the game, with star wide receiver Deebo Samuel pulling his left hamstring and linebacker Dre Greenlaw tearing his Achilles. In my second iteration, I’ll lower the 49ers offensive strength (reducing touchdown and field goal probabilities in favor of punt and turnover probabilities) and lower the 49ers defensive strength (increasing the Chiefs’ touchdown and field goal probabilities and reducing their punt and turnover probabilities), to the extent that the Chiefs are slight favorites. The outcome and associated win probabilities for the 49ers and the Chiefs are shown in Table 6 and Table 7, respectively.
Table 6: Outcome and win probabilities if the 49ers take the ball first, scaling the base case so that the Chiefs are slight favorites heading into overtime.
Table 7: Outcome and win probabilities if the Chiefs have the ball first, scaling the base case so that the Chiefs are slight favorites heading into overtime.
As we can see in the tables above, it is evident that despite adjusting the base case to favor the Chiefs slightly in overtime, the 49ers' probability of winning the Super Bowl declined from 56% to 40.7% when they chose to take the ball first.
What if the Chiefs were sizable favorites?
In my third iteration, with the Chiefs as significant favorites heading into overtime, the 49ers’ Super Bowl win probability dropped from 53.5% to 38.2% when they took the ball first, as evident from Table 8 and Table 9.
Table 8: Outcome and win probabilities if the 49ers take the ball first, scaling the base case so that the Chiefs are significant favorites heading into overtime.
Table 9: Outcome and win probabilities if the Chiefs have the ball first, scaling the base case so that the Chiefs are significant favorites heading into overtime.
Conclusion
For any way I spin it, the 49ers made the wrong decision taking the ball in overtime. From my three iterations we can see that the 49ers lost between 14.6% and 15.3% of their Super Bowl win probability by electing to take the ball first.